In my 42 years of being involved in mathematics education, I think that I have seen it all. Everything from seeing students sitting in straight rows “listening” to the teacher demonstrate to students how to solve a math problem to watching students huddled in groups sharing ideas on how to approach a complex task, and just about every instructional model in-between. And, I have been the educator in each of these models. One thing is for sure, in that I learned so much about what “works” by teaching these lessons that I have taught over the years, and nothing has brought me more joy and continued passion for my profession as a mathematics educator than seeing students choose their own tools, models, and strategies for engaging in mathematics. It is clear to me that when students are passive learners of mathematics that their ownership of the concept is weak and holds little hope of having them remember what they were to do and when and how to use it in the future.
As discussed in the UDL Lesson Plan Makeovers, some mathematics educators have hesitated to engage in learning more about UDL, thinking that it only works for the “other subjects”, often citing concern that losing sight of “I do, we do, you do” instruction or providing choice in how students approach a mathematics task will make for weak foundational learning of mathematics skills. However, when I first began studying Universal Design for Learning (UDL), I realized that what I had found to be my most successful instructional practices for teaching and learning mathematics were inherently interwoven into UDL.
The makeover lessons shared in that same blog provided a beginning step toward recognizing that the UDL principles can be an integral part of how we teach mathematics. In this post, I’d like to take a closer look at how we can go a step further. This mathematics lesson makeover involves fourth-grade students subtracting mixed numbers. The original lesson, from the Eureka Mathematics curriculum, provides a strong mathematical concept foundation for students, however, is strengthened in this makeover by infusing UDL practices. You will see, in this makeover, that students are given a greater opportunity to engage in this content with a personal lens and an opportunity to be active learners through engaging activities and greater choice in the tools that they choose from their mathematics toolbox
Let’s Dive In!
Mathematics Lesson Makeover: 4th Grade Lesson |
|
Orignal Lesson |
UDL Makeover Lesson Plan |
|
Fluency practice task: 1. Sprint (handout in which students time themselves on mental math tasks) 2. Practice (review) problem |
Let’s Do a Number Talk! 1. Choose several problems from the sprint to display on slides for students to view as a group. 2. Students are asked to solve the problem mentally and then volunteer to share how they solved it by describing their strategy. (7.1 Optimize individual choice and autonomy) 3. The teacher passively writes on the board what strategy was used, not commenting on the accuracy or efficiency of the strategy. 4. The entire class reviews the variety of strategies, comparing, discussing accuracy and efficiency. This often leads students to learn new strategies from their peers. (8.3 Foster collaboration and community) |
|
Application Problem The application problem reviews a previously learned concept (decomposition to subtract from a mixed number) in preparation for the concept development. Students are provided with the task in written form. |
You Do, We Do! The teacher may choose to display the application problem on a slide and read the problem to the class, prior to asking them to try solving the problem themselves, using a variety of strategies, rather than the prescribed strategies from the original lesson. (8.2 Vary demands and resources to optimize challenge) An alternative approach would involve leaving out the question (and perhaps the numbers as well) and ask students to begin their work with the application problem by approaching it through a “Numberless Word Problem” format. For those readers who are not familiar with this approach, students are asked to envision the story format, leading to consideration of what operation(s) to use and to eventually choose what the question might be. (source: B. Stockus) (6.2 Support planning and strategy development) |
|
Concept Development The teacher-led whole group engages in various problems involving subtracting a fraction and then a mixed number from a mixed number. Each problem is presented using a given model. Students, at several points, in the lesson are given the opportunity to work with a partner. Students then work on the problem set for 10 minutes. |
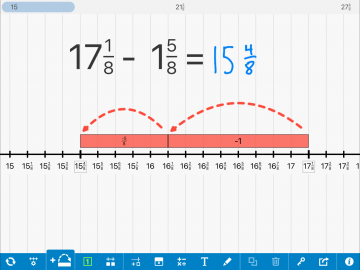
So Many Ways! This segment of the original lesson again involves the teacher leading the class through a variety of strategies for solving the subtraction of mixed number problems. While students do benefit from learning to use a variety of strategies, what is often missing from these original lessons is the opportunity to choose the strategy which best fits the problem. Students should be encouraged to try one or more strategies (and formats within each strategy) to determine which is most effective for them. As an example, the teacher may introduce the use of the number line to solve the problem, a student may more effectively envision the problem using fraction tiles and may be encouraged, eventually by the teacher to compare and relate the two strategies. (1.1 Offer ways of customizing the display of information and 1.3 Offer alternatives for visual information) Here are some mathematical tools that may be used throughout the whole class lesson as well as the completion of the problem set. Use of the number line: 1. Students may be given prepared number lines to use on a handout (along with the problems.) 2. The online number line app from The Math Learning Center is an effective tool for students who benefit from visualizing the model without the need to draw their own. This tool provides a good deal of flexibility, in that students can choose their own units for the number line, start, and endpoints, and can show how they solved the problem with jumps on the number line. Students make take a screenshot of the solution to share with their teacher or display at the end of class for their peers. 3. The kinesthetic model involves students using a physical (or virtual manipulative). The fraction bars (or tiles) are effective for students who need to move the pieces on top of or next to each other in order to envision the subtraction. Students make take a picture (with a tablet) to show their strategic use of the manipulative. There are also a number of virtual manipulative fraction tile apps available which make it easier to subtract problems involving numbers greater than 1, as the number of physical fraction tiles used can become unwieldy for some students. One example may be found on the Didax website and allows students to optionally include a number line with the tiles if they choose to. (4.2 Optimize access to tools and assistive technologies) 4. Some students may find that solving the problems with pencil/paper and do not need to use visual models or manipulatives. These students should not be discouraged from doing so but should be able to provide an explanation, often from drawing a visual model and/or a written solution strategy so that they can recall how they approached the problem. (5.3 Build fluencies with graduated levels of support for practice and performance.) Students often benefit from working with partners once they move to the problem set, however, it is often advantageous to have students try several problems independently first, assuring that they have a starting point for their partner conversations. (9.2 Facilitate personal coping skills and strategies) |
|
Student Debrief Students share answers to the problem set to self-check for accuracy. A guided conversation with teacher-directed questions provides students with the opportunity to share their current understanding. Students are asked to complete a paper-based exit ticket at the end of the lesson. |
What Do You Think? While it is advantageous for students to know which of their answers are correct and which need further exploration, waiting until the debrief to do so often defeats the purpose of working through the class lesson to share and try different strategies if they are incorrect. (8.4 Increase mastery-oriented feedback) Therefore, having answer keys available throughout the lesson is often advantageous. The teacher may choose to highlight one or two problems that she is aware may have given students some difficulty or ask students to share some that they would like to review. During this time, students may share several different strategies, displaying their pictures or their written strategies. If there is adequate time, it is advantageous for the teacher to assist students with providing a comparison of the displayed models and discussing how each leads to the same solution. (3.4 Maximize transfer and generalization) |
|---|---|
|
Homework The homework set asks students to solve several problems using the model demonstrated in the lesson as well as a set of problems in which any solution strategy may be used. |
Reflecting on What We Have Learned Students should be encouraged to try all of the problems in which they have been assigned. As they are attempting the problems, they should be given the opportunity to choose a solution strategy that best suits their needs for each problem. In addition, they may be asked to share why they chose that strategy. Each problem should be attempted, encouraging students to demonstrate their entry points if they struggle to completely solve the problem. If they have difficulty completing the problem, students should be encouraged to write a note explaining their difficulty so that they can remember to share the next day. (9.1 Promote expectations and beliefs that optimize motivation) While some students do benefit from seeing solution strategies shared online while they are working on their homework, either through video or in written form on the teacher’s website, this often leads students to believe that there is only one strategy that is most appropriate. Alternatively, the teacher may choose to share the correct solution for the students to refer to while they are working on their practice problems (as done in class) so that they know whether they are getting a correct solution and can revisit the problem if necessary. Students should be encouraged to share their strategies and solutions through a variety of formats: 1. An effective technological platform, called Classkick, allows students to show their strategies and solutions online, including screenshots of their work. The teacher can choose to turn on the option for students to assist each other if he/she finds it advantageous for the class to work collaboratively. In addition, the teacher can provide constructive feedback to each student individually at any time. (8.4 Increase mastery-oriented feedback and 6.4 Enhance capacity for monitoring progress) Students who solve their homework problems using manipulatives or online materials may choose to share screenshots so that they do not have to redraw their strategies.
|
Take the next step on your learning journey. Learn how to engage in best practices from the Standards for Mathematical Practice and UDL strategies to increase your ability to effectively engage your students in learning elementary mathematics. Discover more about the self-paced course, Mathematics for Everyone: UDL for Elementary Mathematics.
Mathematics for Everyone: UDL for Elementary Mathematics.
Self-Directed Course
30 Continuing Education Hours | Option for 3 Graduate Credits + 15 Additional Hours Upon Completion of Final Project
